Lanjutan logaritma Logaritma
Selamat datang kembali di BLACK MATH, di mana materi matematika akan diulas lebih dalam hingga bagian tergelapnya mueheheheh. sebelumnya kita sudah membahas sedikit tentang logaritma.. dihari yang tenang ini mari kita bahas tentang sifat sifat logaritma.. yuk sahabat hitam belajar bareng..
Sifat-sifat Logaritma
1. Sifat Logaritma dari perkalian
Suatu logaritma merupakan hasil penjumlahan dari dua logaritma lain yang nilai kedua numerus-nya merupakan faktor dari nilai numerus awal. Berikut modelnya:
a log p.q = alog p + alog q
dengan syarat a > 0, 2. Perkalian Logaritma
Suatu logaritma a dapat dikalikan dengan logaritma b jika nilai numerus logaritma a sama dengan nilai bilangan pokok logaritma b. Hasil perkalian tersebut merupakan logaritma baru dengan nilai bilangan pokok sama dengan logaritma a, dan nilai numerus sama dengan logaritma b. Berikut model sifat logaritma nya:
a log b x blog c = alog c
dengan syarat a > 0, 3. Sifat Logaritma dari pembagian
Suatu logaritma merupakan hasil pengurangan dari dua logaritma lain yang nilai kedua numerus-nya merupakan pecahan atau pembagian dari nilai numerus logaritma awal. Berikut modelnya:
a log  = alog p – alog q
= alog p – alog q
dengan syarat a > 0, 4. Sifat Logaritma berbanding terbalik
Suatu logaritma berbanding terbalik dengan logaritma lain yang memiliki nilai bilangan pokok dan numerus-nya saling bertukaran. Berikut modelnya:
a log b = 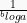
dengan syarat a > 0, 5. Logaritma berlawanan tanda
Suatu logaritma berlawanan tanda dengan logaritma yang memiliki numerus-nya merupakan pecahan terbalik dari nilai numerus logaritma awal. Berikut modelnya:
a log  = – alog
= – alog 
dengan syarat a > 0, 6. Sifat Logaritma dari perpangkatan
Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pengali. Berikut modelnya :
a log bp = p. alog b
dengan syarat a > 0, 7. Perpangkatan Bilangan Pokok Logaritma
Suatu logaritma dengan nilai bilangan pokoknya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pembagi. Berikut modelnya:8. Bilangan pokok logaritma sebanding dengan perpangkatan numerus
Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dari nilai bilangan pokoknya memiliki hasil yang sama dengan nilai pangkat numerus tersebut. Berikut model sifat logaritma nya:
a log ap = p
dengan syarat a > 0 dan 








